“望星楼”里的圆周率
运筹帷幄:预知的计算卡西在《论圆周》一书中得到用十进制小数表示拥有17位准确数字的圆周率,首次打破了祖冲之保持千年之久的记录,直至1596年荷兰数学家鲁道夫(Ludolph,1539~1610)才将用十进制小数表示的圆周率推算至20...
运筹帷幄:预知的计算
卡西在《论圆周》一书中得到用十进制小数表示拥有17位准确数字的圆周率,首次打破了祖冲之保持千年之久的记录,直至1596年荷兰数学家鲁道夫(Ludolph,1539~1610)才将用十进制小数表示的圆周率推算至20位准确数字。今天,借助计算机和更先进的算法,可将圆周率的准确值推算到1000万亿位以上。不断追求卓越是人类与生俱来的天性,我们一定会迎来更加美好的明天。
算法核心:迭代的力量
温馨提示:近期,微信公众号信息流改版。每个用户可以设置 常读订阅号,这些订阅号将以大卡片的形式展示。因此,如果不想错过“中科院之声”的文章,你一定要进行以下操作:进入“中科院之声”公众号 → 点击右上角的 ··· 菜单 → 选择「设为星标」
精美绝伦:完美的算表
人类求解圆周率的历史非常悠久。在数学史上,圆周率的计算方法大体上可以分为两类:早期大多使用的是几何算术方法,即利用多边形逼近单位圆来近似求解;第二类是近现代数学中的解析方法。本文主要讲前者,读者们一般较熟悉的是我国南北朝数学家祖冲之(429~约500),他在《缀术》中将圆周率推算为3.1415926至3.1415927之间。可惜的是《缀术》一书早已遗失,我们并不清楚祖冲之推算圆周率的细节,但幸运的是,约一千年后在遥远的“望星楼”里有一位数学家,他使用了相同的算法将圆周率准确推算到更高的精度,这些完整保存下来的史料为我们展现了古人们的高深智慧。

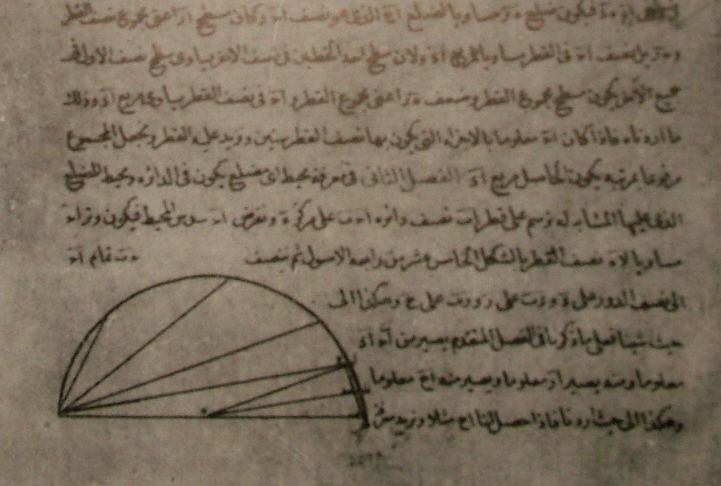
为了天文台工作的开展,乌鲁伯格邀请了当时众多最优秀的科学家在此任教和工作,这其中就包括今天故事的主角——波斯数学家、天文学家阿尔·卡西(al-Kāshī,约1380~1429)。乌鲁伯格给予了卡西很高的评价:“…他(卡西)是一位伟大的科学家,是世界上最优秀的学者之一,他通晓古代科学并且能够推动其发展,他可以解决世界上最困难的问题。”卡西在其1424年成书的《论圆周》(Treatise on the Circumference,1424)中将圆周率准确推算至小数点后第16位。
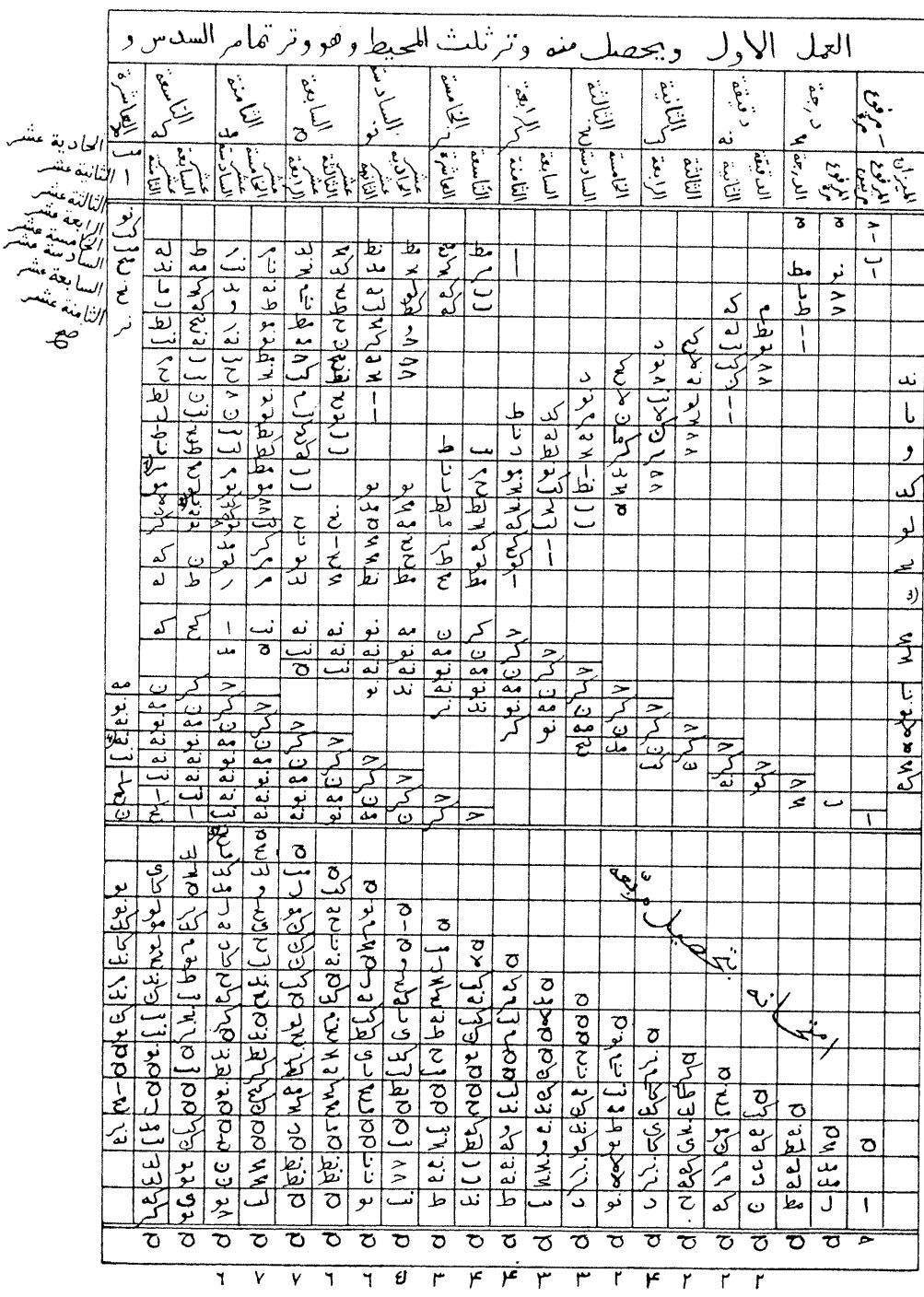
《论圆周》第1张(共28张)迭代开方算表(求3的平方根)
波斯奇才:阿尔·卡西
《丝路山水地图》是明代中后期佚名创作的绢本设色画,描绘了东起嘉峪关西至天方城(麦加)的辽阔地域范围。今天所讲故事的发生地是画中所绘“望星楼”,实际为位于今乌兹别克斯坦第二大城市撒马尔罕的兀鲁伯格天文台。撒马尔罕在突厥语中意为“富裕的村落”,是中亚最古老的城市之一,公元前4世纪已有史书记载,中国古书称之为“康居”“康国”。撒马尔罕座落在连接中国、印度和波斯的陆上丝绸之路的十字路口。1220年,成吉思汗的蒙古铁骑将其攻陷,撒马尔罕遭受了灭顶之灾。转折点是14世纪下半叶,帖木儿(Timur,1336~1405)掌握西察合台汗国的大权,1370年他定都撒马尔罕并将其建为中亚的经济中心。他的孙子乌鲁伯格(Ulugh Beg,公元1394~1449年)统治这里直到1449年,并将其建设成为文化学术中心,兀鲁伯格天文台就是在这一时期修建的。
卡西利用正多边形推算圆周率图示
《隋书·律历志》中关于祖冲之圆周率的记载

卡西的核心工作是连续28张迭代开平方算表。开平方运算对于古代数学家们并不陌生,例如我国秦汉时期数学经典《九章算术》“少广章”中就有关于开平方和开立方的完整论述,但是将高精度开方运算整合在一张算表中在数学史上是很少见的。要保证28张复杂算表中每一个数据的准确性并非易事,为此卡西进行了两类保证其准确性的运算——“弃九法”和平方复原检验法,以做到万无一失。最终卡西计算出2π≈6.2831853071795865。
卡西在《论圆周》介绍部分给出了求解高精度圆周率的原因。他简要回顾了以往三位著名的数学家阿基米德(Archimedes,287~212BC)、阿布·瓦法(Abu’l-Wafā’ ,940~998)和阿尔·比鲁尼(Al-Bīrūnī,973~约1050)相关工作中存在的缺陷。随后,卡西给出了他所要求圆周率的精度要求,即若存在一个直径为地球直径600,000倍的假想天球,使得通过此直径所求得的圆周长与真实值之间的误差小于一根马鬃的粗细。通过估算,卡西得出满足上述要求的圆周率必须精确到60进制分数值的第9位,即60-9(相当于10-16)。换句话说,再将圆周率继续推算几位并不存在技术困难,只是推算至60-9即可。
如果利用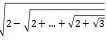 将圆周率推算到60-9(10-16)的精确度,马上就会遇到两个问题:(1)每次迭代开方运算的平方根要精确到什么数位?(2)总共要进行多少次开方(相当于3×2n边形中的n的大小)?通过估算,卡西得到每次开方需要精确到60-18,随后连续进行28次开方运算,相当于利用正3×228边形来逼近圆周。换句话说,如果运算量达不到上述要求,则所求的圆周率精度便不能满足题设,这种事先估算出来的计算量对于后续的求解至关重要。
将圆周率推算到60-9(10-16)的精确度,马上就会遇到两个问题:(1)每次迭代开方运算的平方根要精确到什么数位?(2)总共要进行多少次开方(相当于3×2n边形中的n的大小)?通过估算,卡西得到每次开方需要精确到60-18,随后连续进行28次开方运算,相当于利用正3×228边形来逼近圆周。换句话说,如果运算量达不到上述要求,则所求的圆周率精度便不能满足题设,这种事先估算出来的计算量对于后续的求解至关重要。
伊朗邮票上的阿尔·卡西(左)和苏联邮票上的兀鲁伯格(右)
《论圆周》(1424)首页


中亚明珠:撒马尔罕
揭秘本原:天球与马鬃
卡西算法核心是首先从半径为1的单位圆中的内接正(3×2=)6边形入手,连续利用三角公式推算出圆内接正3×2n边形的边长为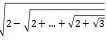 ,将其乘以3×2n边数便可以得出圆内接正多边形周长,正整数n的取值越大,此内接多边形的周长越接近圆周。类似地,卡西构造了另一个与之相似的圆外切正多边形,二者共同逼近圆周,最后用二者的算术平均数来表示单位圆周长,即2倍圆周率。上述算法思想与中国传统数学中的“割圆术”相似。
,将其乘以3×2n边数便可以得出圆内接正多边形周长,正整数n的取值越大,此内接多边形的周长越接近圆周。类似地,卡西构造了另一个与之相似的圆外切正多边形,二者共同逼近圆周,最后用二者的算术平均数来表示单位圆周长,即2倍圆周率。上述算法思想与中国传统数学中的“割圆术”相似。
《丝路山水地图》(局部)中的“望星楼”(左)与兀鲁伯格天文台遗址(右)
卡西在《算术之钥》(1427)中关于“弃九法”的论述

来源:中国科学院自然科学史研究所

今天出了一个新闻:今年,全国高校毕业生预计总量是874万,比去年增加40万。上海高校毕业生预计总量是19.3万人,比去年增加0.3万人。其中:研究生4.9万人,与去年持平;本科生9.8万人,增加0.5万人;专科高职生4.6万人,下降0.2万人 ...
法律法规网消息 黎曼猜想在数学里面是非常重要的猜想,目前还没有确切的权威证明猜想已经被证明,但去年这位数学界称已经证明猜想而且引起了很人验证。
当地时间1月11日,英国皇家学会发布讣告称,数学家迈克尔阿蒂亚爵士(S ...
法律法规网消息 据英国媒体报道,数学家迈克尔阿蒂亚爵士(Sir Michael Francis Atiyah)已经离开了人世,享年89岁。他是如何去世的?家人如何回应此事?回顾生前事迹!
阿蒂亚于1929年4月22日出生于英国伦敦,现年89岁。他的父亲 ...
新华社德国海德堡9月24日电(记者沈忠浩)现年89岁的英国著名数学家、阿贝尔奖和菲尔兹奖得主迈克尔·阿提亚24日在德国海德堡提出了证明黎曼猜想的“简单思路”,并称沿着该思路可以证明黎曼猜想。这一说法震动了数学界和社交媒体 ...
9月18日,阿里发布了数学计划:举办数学大赛,号召全社会的年轻人热爱数学,从这门基础科学中发现新知。晚间,阿里巴巴董事局主席马云,在杭州的阿里西溪园区,跟11位全球顶尖数学家做了一次90分钟的交流。这些数学家来自中国、英 ...